Question

Given the graph of f'(x) shown below, find the intervals on which the function f(x) is increasing.

See the graph attached below.

Isn't the answer supposed to be (-infinity, -2) U (1, infinity) ?

Answer 1

intervals (-3,-1) and (0,+infinity)

Explanation:

if f'(x)>0 then f is increasing

Answer 2

f(x) is increasing on the intervals (-4, -3), (-2, -1),
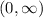`\((0, \infty)\)`, and the intervals where f'(x) > 0 on the x-axis.

To determine the intervals on which the function y = f(x) is increasing, we can analyze the graph of f'(x), which represents the derivative of f(x).

From the given graph of f'(x):

1. It starts between 0 and 1 on the x-axis and 4 on the y-axis.

2. Passes through the point (1, 2).

3. Increases to between 3 and 4 on the x-axis and 3 on the y-axis.

The intervals on which f(x) is increasing correspond to the intervals where f'(x) > 0, as the derivative indicates the rate of change.

Based on the given information:

1. f'(x) > 0 between 0 and 1 on the x-axis.

2. f'(x) > 0 between 3 and 4 on the x-axis.

These intervals suggest that f(x) is increasing on the corresponding intervals.

Now, let's consider the inverted U-shaped curve for f(x) with the given points (-4, -2), (-3, 0), (-2, -1), (-1, 0), and (0, -2). Between these points, the function f(x) is increasing.

Therefore, the intervals on which f(x) is increasing are (-4, -3), (-2, -1), and
`\((0, \infty)\).`