9514 1404 393
Answer:
odd
Explanation:
An odd function has the characteristics ...
- symmetrical about the origin
- f(-x) = -f(x)
An even function has the characteristics ...
- symmetrical about the y-axis
- f(-x) = f(x)
__
The graph of the function shows symmetry about the origin. If we substitute -x for x, we get ...
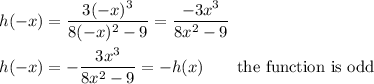
_____
Additional comment
Both the numerator and denominator are polynomial functions. A polynomial function is odd if it contains only odd-degree terms, like the function in the numerator. A polynomial function is even if it contains only even-degree terms, like the function in the denominator. (A constant is 0 degree--even.)
A rational function consisting of the ratio of odd or even functions (not "neither"), will be odd or even according to the parity of the ratio:
odd/odd = even/even = even function
odd/even = even/odd = odd function . . . . . the situation in this problem