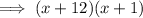Answer:
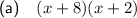
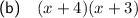
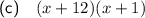
Explanation:
Factoring quadratics
- To factor a quadratic in the form
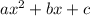 find two numbers that multiply to
find two numbers that multiply to
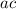 and sum to
and sum to
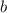 .
. - Rewrite
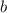 as the sum of these two numbers.
as the sum of these two numbers. - Factor the first two terms and the last two terms separately.
- Factor out the common term.
Part (a)
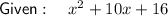
Two numbers that multiply to 16 and sum to 10 are: 2 and 8.
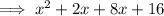
Factor the first two terms and the last two terms separately:
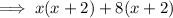
Factor out the common term (x + 2):
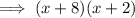
Part (b)
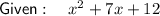
Two numbers that multiply to 12 and sum to 7 are: 3 and 4.
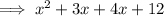
Factor the first two terms and the last two terms separately:
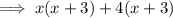
Factor out the common term (x + 3):
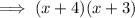
Part (c)
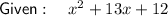
Two numbers that multiply to 12 and sum to 13 are: 1 and 12.
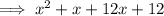
Factor the first two terms and the last two terms separately:
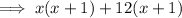
Factor out the common term (x + 1):