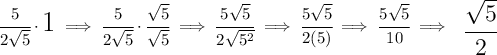Question

How to simplify:


`(5)/(2√(5) )`

My textbook says the answer is
`(√(5) )/(2)`, but I don't know to get there.
Someone pls help

Answer 1

hmmm first of all, let's keep in mind that any expression multiplied by 1 is always the same expression

`12\cdot 1=12\qquad 13567\cdot 1=13567\qquad spaghetti\cdot 1=spaghetti`

and so on.

now, hmm 1 can be expressed as a rational, 1/1 = 1, but but but, we can really express it as

`\cfrac{9999}{9999}\implies \cfrac{7857}{7357}\implies \cfrac{\sqrt[11]{1375}}{\sqrt[11]{1375}}\implies \cfrac{spaghetti}{spaghetti}\implies \cfrac{lettuce}{lettuce}\implies \text{\Huge 1}`

so let's do the so-called rationalizing of the denominator, we can also do it with the numerator btw, but we only need it for the denominator right now, by multiplying for 1 :), 1 is Da Bomb baby!!

`\cfrac{5}{2√(5)}\cdot \text{\LARGE 1}\implies \cfrac{5}{2√(5)}\cdot \cfrac{√(5)}{√(5)}\implies \cfrac{5√(5)}{2√(5^2)}\implies \cfrac{5√(5)}{2(5)}\implies \cfrac{5√(5)}{10}\implies {\Large \begin{array}{llll} \cfrac{√(5)}{2} \end{array}}`