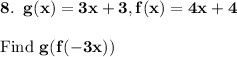Answer:
5.
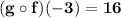
6.
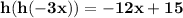
7.

8.
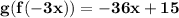
Explanation:
These are examples of composite functions.
What is a composite function?
A function by definition is a process that takes a collection of inputs and produces a corresponding collection of outputs in such a way that the process produces one and only one output value for any single input value.
Since we consider a function a process it makes sense to think of two functions acting in sequence to produce a single output. The output from one function is fed into the second function.
- A composite function can be written as:
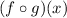
- The above can also be written as
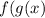
- This means the output of function
 is fed as input to function
is fed as input to function
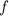
- We refer to g as the inner function and f as the outer function
- The evaluation goes from inner to outer so first
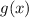 is evaluated and the result fed to
is evaluated and the result fed to
 as input which produces the composite result
as input which produces the composite result
Note that we can have
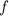
 as the outer function, in which case the notation will be
as the outer function, in which case the notation will be
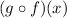 or
or

Problem Solution
5.
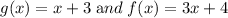
Find
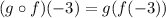
- First compute f(-3) in
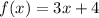
⇒ 3(3) + 4 = 9 + 4 = 13
- Then use this value for
 in
in
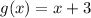
⇒ 13 + 3 = 16
-
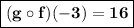
6.
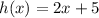
Find
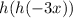
- Here the output of h is fed into h again but the process of evaluation is the same
- h(-3x) in h(x) = 2x + 5
Substitute -3x wherever you see an x
=> 2 (-3x) + 5 => -6x + 5 - Feed this into h again
h((-3x)) = h(-6x + 5)
= 2(-6x + 5) + 5
= -12x +10 + 5
= -12x + 15
-
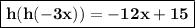

.