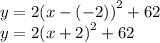Question

5. Rewrite the quadratic funtion from standard form to vertex form.
Ax) = 2x2 + 8x + 70

Answer 1

`y = 2 {(x + 2)}^(2) + 62`

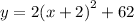
Explanation:

vertex form is

`y = a {(x - h)}^(2) + k \\ where \: (h. \: k) \: is \: the \: vertex`

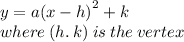
our original equation

`2 {x}^(2) + 8x + 70`

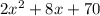
first we will find the x value using the formula

`x = - (b)/(2a) \\ - (8)/(2(2)) = - (8)/(4) = - 2 \\ x = - 2 = h`

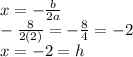
plug the value of x back into the original equation to solve for y

`y = 2 {x}^(2) + 8x + 70 \\ y = 2 ({ - 2}^(2) ) + 8( - 2) + 70 \\ y = 2(4) - 16 + 70 \\ y = 8 - 16 + 70 \\ y = 78 - 16 \\ y = 62 = k`

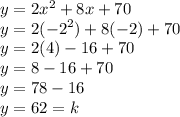
substitute this back into our vertex form and not forgetting the coefficient a = 2

`y = 2 {(x - ( -2))}^(2) + 62 \\ y = 2 {(x + 2)}^(2) + 62`