Question

The sidewalks at a park can be modeled by the equations:3(y+1)=2x,2y-8=-3x,2x+3=3y,and "-2(y-12)=3x." Determine the slopes of the equations,and then use them to classify the quadrilateral bounded by the sidewalks.

Answer 1

Slopes: ²/₃ and -³/₂

Quadrilateral: Rectangle

Explanation:

Given equations:

`\begin{cases}3(y+1)=2x\\2y-8=-3x\\2x+3=3y\\-2(y-12)=3x\end{case}`

Slope-intercept form of a linear equation

`\boxed{y=mx+b}`

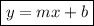
Where:

• m is the slope.
• b is the y-intercept.

To determine the slopes of the given equations, rearrange them to isolate y.

`\begin{aligned}\textsf{Equation 1}: \quad 3(y+1)&=2x\\(3(y+1))/(3)&=(2x)/(3)\\y+1&=(2)/(3)x\\y+1-1&=(2)/(3)x-1\\y&=(2)/(3)x-1\\\end{aligned}`

`\begin{aligned}\textsf{Equation 2}: \quad \quad2y-8&=-3x\\2y-8+8&=-3x+8\\2y&=-3x+8\\(2y)/(2)&=(-3x)/(2)+(8)/(2)\\y&=-(3)/(2)x+4\\\end{aligned}`

`\begin{aligned}\textsf{Equation 3}: \quad 2x+3&=3y\\3y&=2x+3\\(3y)/(3)&=(2x)/(3)+(3)/(3)\\y&=(2)/(3)x+1\end{aligned}`

`\begin{aligned}\textsf{Equation 4}: \quad -2(y-12)&=3x\\(-2(y-12))/(-2)&=(3x)/(-2)\\y-12&=-(3)/(2)x\\y-12+12&=-(3)/(2)x+12\\y&=-(3)/(2)x+12\end{aligned}`

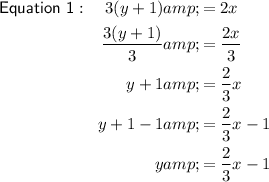
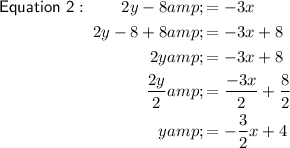
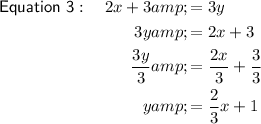
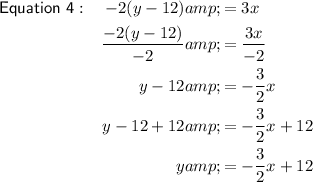
The slopes of Equation 1 and Equation 3 are the same: ²/₃

The slopes of Equation 2 and Equation 4 are the same: -³/₂

If two lines are parallel, the slopes are the same.

Therefore, the opposite sides of the quadrilateral bounded by the lines are parallel.

-³/₂ is the negative reciprocal of ²/₃.

If two lines are perpendicular (intersect at a right angle), the slopes are negative reciprocals (multiply to -1).

Therefore, all the interior angles of the quadrilateral bounded by the lines are 90°.

As the opposite sides of the quadrilateral are parallel and its interior angles are 90°, the quadrilateral bounded by the sidewalks is a rectangle.