Question

Simple Arithmetic Sequence Problem
Can someone explain this?

Answer 1

see explanation

Explanation:

(a)

given the arithmetic series 5 + a + 14 + b

the difference between consecutive terms is constant , that is

a₂ - a₂ = a₃ - a₂ ( substitute values )

a - 5 = 14 - a ( add a to both sides )

2a - 5 = 14 ( add 5 to both sides )

2a = 19 ( divide both sides by 2 )

a = 9.5

then

a₄ - a₃ = a₂ - a₁

b - 14 = a - 5 = 9.5 - 5 = 4.5 ( add 14 to both sides )

b = 18.5

(b)

the sum to n terms of an arithmetic series is

`S_(n)` =
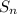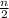`(n)/(2)` [ 2a₁ + (n - 1)d ]

where a₁ is the first term and d the common difference

here a₁ = 5 and d = a₂ - a₁ = 14 - a = 14 - 9.5 = 4.5 , then

S₁₀ =
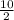`(10)/(2)` [ (2 × 5) + (9 × 4.5) ]

= 5(10 + 40.5)

= 5 × 50.5

= 252.5

(c)

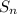`S_(n)` > 500 , that is

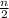`(n)/(2)` (50.5) > 500 ( multiply both sides by 2 )

50.5n > 1000 ( divide both sides by 50.5 )

n > 19.80198... , that is

n = 20