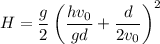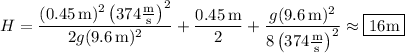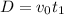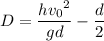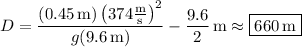1 Answer

Prakash Thapa · Answer 1 · 2022-01-16T13:45:47+0000

Judging by the sketch, H is the vertical distance and D is the horizontal distance between where the bullet is shot and where it gets lodged in the wall. Let v₀ = 374 m/s, h = 0.45 m, and d = 9.6 m.

At time t, the bullet has

• horizontal position

x = v_0 t

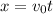
• vertical position

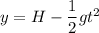
$y = H - \frac12 gt^2$

Let t₁ and t₂ be the times when the bullet reaches the window and the wall, respectively. We want to find H and D given that

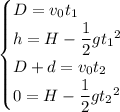
$\begin{cases}D = v_0 t_1 \\ h = H - \frac12 g {t_1}^2 \\ D + d = v_0 t_2 \\ 0 = H - \frac12 g {t_2}^2\end{cases}$

Eliminate D and H to get a system of equations involving t₁ and t₂ :

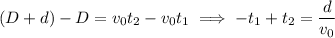
$(D + d) - D = v_0 t_2 - v_0 t_1 \implies -t_1 + t_2 = \frac d{v_0}$

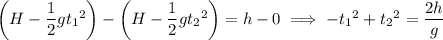
$\left(H - \frac12 g {t_1}^2\right) - \left(H - \frac12 g {t_2}^2\right) = h - 0 \implies -{t_1}^2 + {t_2}^2 = \frac{2h}g$

The first of these equations says

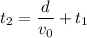
$t_2 = \frac d{v_0} + t_1$

and substituting into the second equation gives

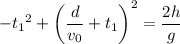
$-{t_1}^2 + \left(\frac d{v_0} + t_1\right)^2 = \frac{2h}g$

Solve for t₁ :

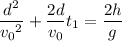
$\frac{d^2}{{v_0}^2} + (2d)/(v_0) t_1 = \frac{2h}g$

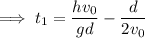
$\implies t_1 = (hv_0)/(gd) - (d)/(2v_0)$

Solve for t₂ :

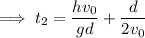
$\implies t_2 = (hv_0)/(gd) + (d)/(2v_0)$

Now solve for H and D :

$H = \frac12 g {t_2}^2$

$H = \frac g2 \left((hv_0)/(gd) + (d)/(2v_0)\right)^2$

$H = \frac{h^2{v_0}^2}{2gd^2} + \frac h2 + \frac{gd^2}{8{v_0}^2}$

$H = ((0.45\,\mathrm m)^2 \left(374(\rm m)/(\rm s)\right)^2)/(2g(9.6\,\mathrm m)^2) + \frac{0.45 \,\rm m}2 + (g(9.6\,\mathrm m)^2)/(8\left(374(\rm m)/(\rm s)\right)^2) \approx \boxed{16 \mathrm m}$