Question

Write the equation of the line in slope intercept form that goes through (5,4) and is

parallel to −4x + y = 5

Answer 1

`{ \qquad\qquad\huge\underline{{\sf Answer}}}`

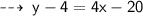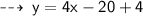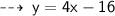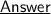
Here we go ~

First, let's find slope of line parallel to required line by converting the equation into slope intercept form :

`\qquad \sf  \dashrightarrow \: - 4x + y = 5`

`\qquad \sf  \dashrightarrow \: y = 4x + 5`

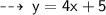
So, it's slope is 4 ( Coefficient of x )

Slope of required line is equal to the line parallel to it, so slope of required line is 4 as well.

Now, we have slope : m = 4, and it passes through point (5 , 4) so let's write it's equation in point slope form ~

`\qquad \sf  \dashrightarrow \: y - y _ 1 = m(x - x _ 1)`

`\qquad \sf  \dashrightarrow \: (y -4) = 4(x - 5)`

`\qquad \sf  \dashrightarrow \: y - 4 = 4x - 20`

`\qquad \sf  \dashrightarrow \: y = 4x - 20 + 4`

`\qquad \sf  \dashrightarrow \: y = 4x - 16`