Answer:
28,339 lbs
Explanation:
If the lifting force exerted on an airplane wing varies jointly as the area of the wing's surface and the square of the plane's velocity then:
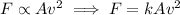
Where:
- F = lifting force in pounds (lbs)
- A = area in square feet (ft²)
- v = velocity in miles per hour (mph)
- k = some constant
Given:
- F = 10,500 lbs
- A = 180 ft²
- v = 140 mph
Substitute the given values into the found equation and solve for k (variation constant):

Therefore:

To find the lifting force (F) when the plane speeds up to 230 mph, substitute the given area of the wing (A = 180 ft²) and the new velocity (v = 230 mph) into the equation and solve for F:
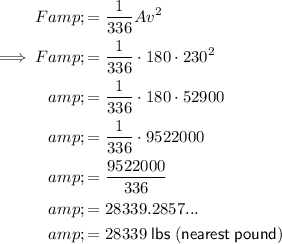
Therefore, the lifting force is 28,339 lbs (nearest pound).