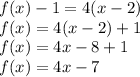Question

Write the equation for the tangent line to the
graph of f(x) = x2 – 3 where x = 2

Answer 1

The equation of a tangent line is y = 4x-7

Explanation:

We are given our quadratic function:-

`\displaystyle \large{f(x) = {x}^(2) - 3}`

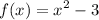
Since we want to find a line that is tangent to the parabola, let's recall our basic differential.

Differential (Power/Exponent)

`\displaystyle \large{f(x) = a {x}^(n) \longrightarrow f'(x) = na {x}^(n - 1) }`

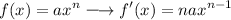
Differential (Constant)

`\displaystyle \large{f(x) = a \longrightarrow f'(x) = 0}`

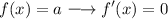
For a = constant.

First, differentiate the function.

`\displaystyle \large{f(x) = {x}^(2) - 3} \\ \displaystyle \large{f'(x) = 2{x}^(2 - 1) - 0} \\ \displaystyle \large{f'(x) = 2x}`

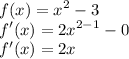
Then substitute x = 2 in f'(x) to find the slope at x = 2 for parabola.

`\displaystyle \large{f'(2)= 2(2)} \\ \displaystyle \large{f'(2)= 4}`

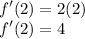
Therefore, slope at x = 2 is 4.

Form a point-slope equation:-

Point-Slope (Derivative)

`\displaystyle \large{f(x) - f(a) = f'(a)(x - a)}`

Let a = x = 2

To find f(a), substitute x = a = 2 in x^2-3.

`\displaystyle \large{f(2) = {2}^(2) - 3} \\ \displaystyle \large{f(2) = 4- 3} \\ \displaystyle \large{f(2) = 1}`

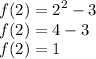
Therefore our f(a) is 1.

We know:-

• f(a) = 1
• a = 2
• f'(a) = 4

Therefore the tangent equation is:-

`\displaystyle \large{f(x) - 1 = 4(x - 2)} \\ \displaystyle \large{f(x) = 4(x - 2) + 1} \\ \displaystyle \large{f(x) = 4x - 8 + 1} \\ \displaystyle \large{f(x) = 4x - 7}`