Question

46. Mean of n observations is š. If each of these

observations is increased by 1, 2, 3, 4...n, respec-
tively, then what will be their mean?

Answer 1

Answer: S+0.5(n+1)

==============================================================

Step-by-step explanation:

Consider the set

`\left\{x_1,x_2,x_3,\ldots,x_n\right\}\\\\`

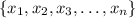
which has n items in it. We don't know anything about any individual item, but what we do know is that the mean is S.

So,

`\text{mean} = \frac{\text{sum of values}}{\text{number of values}}\\\\\text{mean} = (x_1+x_2+x_3+\ldots+x_n)/(n)\\\\S = (x_1+x_2+x_3+\ldots+x_n)/(n)\\\\nS = x_1+x_2+x_3+\ldots+x_n\\\\x_1+x_2+x_3+\ldots+x_n = nS\\\\`

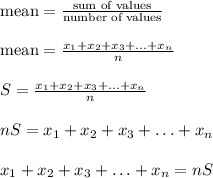
In short, the sum of the values
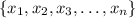`\left\{x_1,x_2,x_3,\ldots,x_n\right\}\\\\` is exactly nS, where S is the mean of the same set.

------------------------

Next, we add 1 to
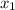`x_1`, add 2 onto
`x_2`, etc to form this new set

`\left\{x_1+1,x_2+2,x_3+3,\ldots,x_n+n\right\}\\\\`

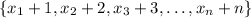
Let's find the mean like so

`\text{mean} = \frac{\text{sum of values}}{\text{number of values}}\\\\\text{mean} = ((x_1+1)+(x_2+2)+(x_3+3)+\ldots+(x_n+n))/(n)\\\\\text{mean} = (\left(x_1+x_2+x_3+\ldots+x_n\right)+\left(1+2+3+\ldots n\right))/(n)\\\\\text{mean} = (nS+0.5n(n+1))/(n)\\\\\text{mean} = (n(S+0.5(n+1)))/(n)\\\\\text{mean} = S+0.5(n+1)\\\\`

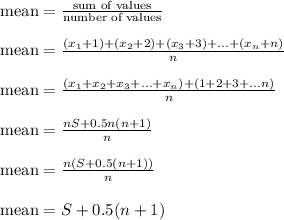
which is why S+0.5(n+1) is the answer

------------------------

Let's look at a concrete example.

Consider the set {1,7,10} which has n = 3 items in it.

Its mean is,

S = (1+7+10)/3 = 18/3 = 6

Now increase the items in {1,7,10} by adding on the values {1,2,3} to each element in the order shown

1+1 = 2

7+2 = 9

10+3 = 13

So {1,7,10} becomes {2,9,13}

The mean of the new set {2,9,13} is...

mean = (2+9+13)/3 = 24/3 = 8

Notice how,

newMean = S + 0.5(n+1)

newMean = 6 + 0.5(3+1)

newMean = 8

which helps us see how the formula works and partially confirm the answer. While this example isn't definitive proof, it's still handy to go over. I recommend forming other sets to check to see that this formula works. Not only do I recommend trying different values, but also a different number of values as well (i.e. increase n to some larger integer).