Answer:
1) 9.83 m/s (2 d.p.)
2) 0.04 km (2 d.p.)
Step-by-step explanation:
Constant Acceleration Equations (SUVAT)

When using SUVAT, assume the object is modeled as a particle and that acceleration is constant.
Part 1
Given:
- u = 22.1 km/h
- a = 0.84 m/s²
- t = 4.4 s
Convert km/h into m/s by dividing by 3.6:
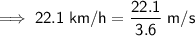
Substitute the given values into the formula and solve for v:

Therefore, the final speed of the car was 9.83 m/s (2 d.p.).
Part 2
Substitute the given values into the formula and solve for s, remembering to use the initial velocity in m/s:
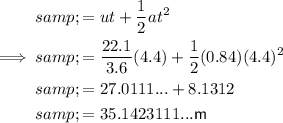
Convert meters into kilometers by dividing by 1000:
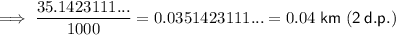
Therefore, the displacement of the car after 4.4 s was 0.04 km (2 d.p.).