Prerequisites :-
1) The product of slope of two perpendicular lines is-1 .
2) The slope of two parallel lines is same .
Given two lines to us are ,
This line is in slope intercept form which is
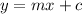 . Comparing to which we get ,
. Comparing to which we get ,
Again , the second line given to us is ,
Convert it into slope intercept form , we have ,
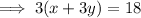
Divide both sides by 3 ,
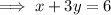
Solve for y ,
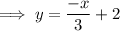
On comparing to the slope intercept form ,
And the product both the slopes is ,
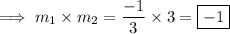
Hence the given two lines are perpendicular .