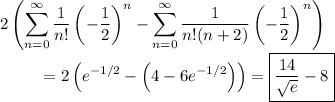Expand into partial fractions,
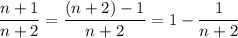
and rewrite the sum as
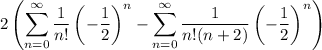
The first sum we recognize as the series expansion of
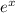 at
at
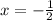 . For the other sum, let
. For the other sum, let
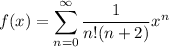
Introduce factors of
 so that differentiating both sides will eliminate the
so that differentiating both sides will eliminate the
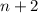 in the denominator of the summand.
in the denominator of the summand.
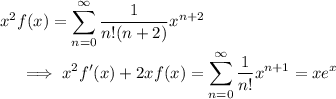
Solve the differentiating equation for
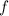 , using the initial condition
, using the initial condition
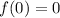 .
.
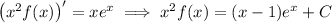
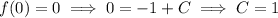
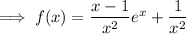
Now let
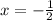 . We find
. We find