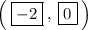Answer:
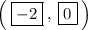
Explanation:
Given system of equations:
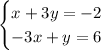
To solve using the method of substitution, solve one equation for one of the variables.
Solving equation 2 for y:
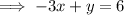
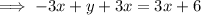
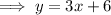
Substitute this expression into the other equation and solve for x:
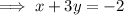
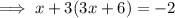
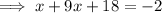
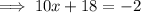

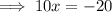
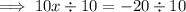
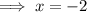
Substitute the found value of x into the expression for y, and solve for y:
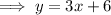
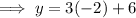
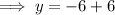
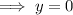
Therefore, the solution to the given system of equations is: