Question

Match the statements defined below with the letters labeling their equivalent expressions.

1. |x−4|=8
2. |x−4|≥8
3. |x−4|>8
4. |x−4|<∞
5. |x−4|≤8

A. x∈(−∞,∞)
B. x∈[−4,12]
C. x∈(−∞,−4)∪(12,∞)
D. x∈(−∞,−4]∪[12,∞)
E. x∈{−4,12}

Answer 1

Use the definition of absolute value to rewrite each equation or inequality.

`|x| = \begin{cases} x & \text{if } x\ge0 \\ -x & \text{if }x < 0 \end{cases}`

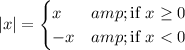
1. (E) From the definition it follows that

`x-4 \ge 0 \implies |x-4| = x-4 = 8 \implies x = 12`

`x-4 < 0 \implies |x-4| = -(x-4) = 4-x = 8 \implies x = -4`

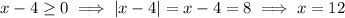
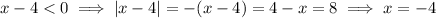
Then the solution set contains exactly 2 elements, and we write it as shown in choice (E),
`x\in\{-4,12\}`.

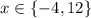2. (D) We solve the inequality in essentially the same way as in (1), we just need to keep track of the direction of the inequality.

`x-4\ge0 \implies|x-4|=x-4\ge8 \implies x\ge12`

`x-4<0 \implies|x-4|=4-x\ge8 \implies x\le-4`

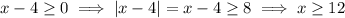
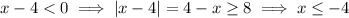
Note the inclusion of
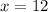`x=12` and
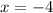`x=-4`. We write this as a union of two half-closed intervals,
`x\in(-\infty,-4]\cup[12,\infty)`.

3. (C) This follows from the same steps as in (2). This time the inequality is strict, so we exclude the endpoints and with open intervals write
`x\in(-\infty,4)\cup(12,\infty)`.

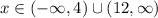4. (A) Since
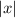`|x|` always returns a non-negative number, any real number
`x` satisfies the inequalty
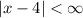`|x-4|<\infty`. We write the solution set as the entire real line,
`x\in(-\infty,\infty)`.

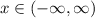5. This leaves us with (B) for the last solution set. This inequality is complementary to the one in (3), which means the solution set to
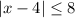`|x-4|\le8` is the complement of the set we found in (3). That interval removes everything between and including -4 and 12 from the real line. So the solution in this case is what we omit from the solution to (3), and we write
`x\in[-4,12]`.