Recall the beta function definition and gamma identity,
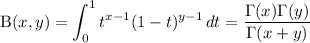
Consider the sum
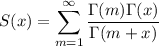
Compute it by converting the gammas to the beta integral, interchanging summation with integration, and using the sum of a geometric series.
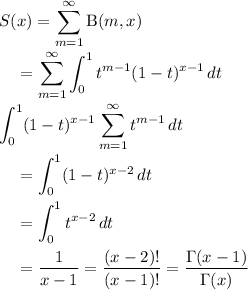
It follows that
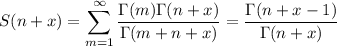
Now we compute the sum of interest. It's just a matter of introducing appropriate gamma factors to condense the double series into a single hypergeometric one.
Recall the definition of the generalized hypergeometric function,
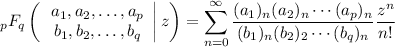
where
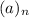 denotes the Pochhammer symbol, defined by
denotes the Pochhammer symbol, defined by
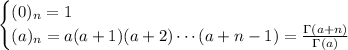
We'll be needing the following identities later.
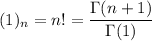
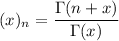
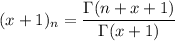
The
 -sum is
-sum is
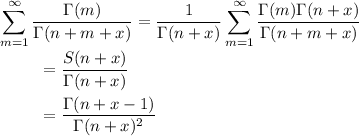
Then the double sum reduces to

Rewrite the summand. We use the property
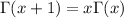 to convert to Pochhammer symbols.
to convert to Pochhammer symbols.
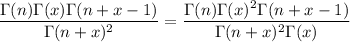
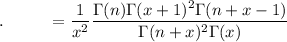

![\displaystyle . ~~~~~~~~ = \frac1{x^2} ((n-1)! (x)_(n-1))/(\left[(1+x)_(n-1)\right]^2)](https://img.qammunity.org/2023/formulas/mathematics/college/acfr6vdkjbfozwtn0gkwjwcf1l5dutvf4h.png)
Now in the sum, shift the index to start at 0, and introduce an additional factor of
 to get the hypergeometric form.
to get the hypergeometric form.
![\displaystyle \sum_(n=1)^\infty \frac1{x^2} ((n-1)! (x)_(n-1))/(\left[(1+x)_(n-1)\right]^2) = \frac1{x^2} \sum_(n=0)^\infty ((n!)^2 (x)_n)/(\left[(1+x)_n\right]^2) \frac1{n!} \\\\ ~~~~~~~~ = \frac1{x^2} \sum_(n=0)^\infty ([(1)_n]^2 (x)_n)/(\left[(1+x)_n\right]^2) \frac1{n!} \\\\ ~~~~~~~~ = \boxed{\frac1{x^2} \, {}_3F_2\left(\left.\begin{array}{c}1,1,x\\1+x,1+x\end{array}\right\vert1\right)}](https://img.qammunity.org/2023/formulas/mathematics/college/sbmkf8mjwcu582mojvdk0poj47vuvkhkdu.png)