Since
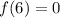 , by the remainder theorem this means that x - 6 divides f(x) exactly. This means there are constants a, b, and c such that
, by the remainder theorem this means that x - 6 divides f(x) exactly. This means there are constants a, b, and c such that
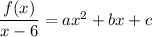
Multiplying both sides by x - 6 gives

Then a, b, c satisfy
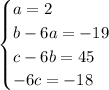
and solving this system gives a = 2, b = -7, and c = 3.
So, we have
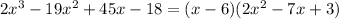
The quadratic term can be factored as
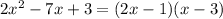
which leaves us with
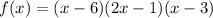
so that the zeros of f(x) are 6, 1/2, and 3.