Question

How do you solve 1/4(x+5)^2-1=3 in steps?

Answer 1

`{ \tt{ (1)/(4) (x + 5) {}^(2) - 1 = 3 }} \\ \\ { \tt{ (1)/(4) {(x + 5)}^(2) = 4 }} \\ \\ { \tt{ {(x + 5)}^(2) = 16 }} \\ \\ { \tt{ \sqrt{ {(x + 5)}^(2) } = √(16) }} \\ \\ { \tt{x + 5 = ±4}} \\ \\ { \tt{x = ±4 - 5}} \\ \\ { \boxed{ \tt{ \: \: x = {}^( - )1 \:or \:-9 }}}`

Answer 2

x = -1, -9

Explanation:

given:

1/4(x+5)^2-1=3

rewriting:

`(1)/(4) (x+5)^2-1=3`

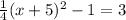
add 1 to both sides:

`(1)/(4) (x+5)^2 = 4`

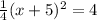
divide both sides by 1/4:

`(x+5)^2 = 16`

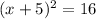
square root both sides:

`x + 5 = + / - 4`

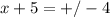
subtract 5 from both sides, we now have two equations to solve:

x = - 5 - 4 x = - 5 + 4

x = -9 x = - 1

answer:

x = -1, -9

Hopefully this helps, have a nice day! :D

Edit: The other answer forgot to solve for when 4 is negative

Edit #2: They have fixed it now