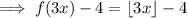Answer:
6. Stretched horizontally by a factor of 1/2 and stretched vertically by a factor of 4.
7. Stretched horizontally by a factor of 1/3 and translated 4 units down.
Explanation:
Transformations
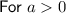
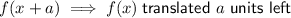

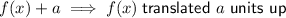

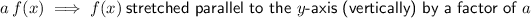
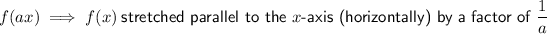

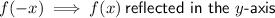
Question 6
Parent function:
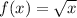
Stretched horizontally by a factor of 1/2:
Multiply the x-variable by 2:
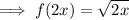
Stretched vertically by a factor of 4:
Multiply the function by 4:
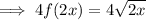
Question 7
Parent function:

Stretched horizontally by a factor of 1/3:
Multiply the x-variable by 3:

Translated 4 units down:
Subtract 4 from the function: