Answer:
B
Explanation:
There are several ways to find the vertex of function such as formula, completing the square or differential.
I will use the formula to find the vertex.
We are given the function:

Vertex Formula
Let (h,k) = vertex
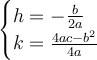
From the function, compare the coefficients:
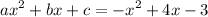
Therefore:-
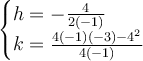
Then evaluate for h-value and k-value.
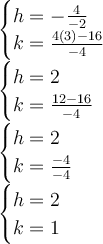
Therefore the vertex is (h,k) = (2,1)