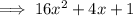Answer:
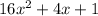
Explanation:
Given expression:
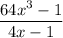
Step 1
Factor the numerator of the given expression.
Rewrite 64 as 4³ and 1 as 1³:
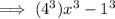
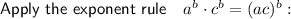
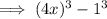
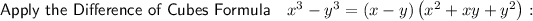
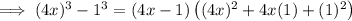
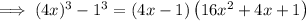
Step 2
Replace the numerator in the given expression with the factored numerator from step 1:
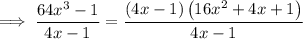
Cancel the common factor (4x - 1):