Question

A rubber ball is dropped from the top of a hole. Exactly 2.5 seconds later, the sound of the rubber ball hitting bottom is heard. How deep is the hole?

(Hint: The distance that a dropped object falls in t seconds is represented by the formula s = 16². The speed of sound is 1100 ft/sec.)

Answer 1

The depth of the hole is approximately 93.33 feet.

To solve this problem, we need to account for two key components: the time it takes for the ball to fall to the bottom of the hole and the time it takes for the sound to travel back up the hole. The total time for these two events is 2.5 seconds.

Let's denote:

-
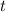`\( t \)` as the time in seconds it takes for the ball to hit the bottom.

-
`\( d \)` as the depth of the hole in feet.

The distance an object falls in
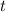`\( t \)` seconds is given by the formula
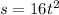`\( s = 16t^2 \)` (where
`\( s \)` is in feet). Therefore, the depth of the hole (distance the ball falls) is
`\( d = 16t^2 \)`.

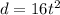The speed of sound is 1100 ft/sec. So, the time it takes for the sound to travel back up the hole is
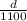`\( (d)/(1100) \)` seconds.

Since the total time for the ball to drop and the sound to return is 2.5 seconds, we have:

`\[ t + (d)/(1100) = 2.5 \]`

Now we can substitute
`\( d \)` with
`\( 16t^2 \)` in the above equation:

`\[ t + (16t^2)/(1100) = 2.5 \]`

We'll solve this equation for
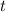`\( t \)` to find the time it takes for the ball to hit the bottom and then use
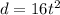`\( d = 16t^2 \)` to find the depth of the hole. Let's calculate:

After solving the equation, we find that the time
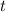`\( t \)` it takes for the ball to hit the bottom of the hole is approximately 2.42 seconds. Using this time, the depth of the hole
`\( d \)` can be calculated using the formula
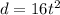`\( d = 16t^2 \)`. Substituting
`\( t = 2.42 \)` seconds into this formula gives us:

`\[ d = 16 * (2.42)^2 \approx 93.33 \text{ feet} \]`

Therefore, the depth of the hole is approximately 93.33 feet.