Question

What is the slope of the line that passes through the points (2, -4) and (5, 2)? Write

your answer in simplest form.

Answer 1

Slope: 2

The slope how much y increases when x increases by 1.

Explanation:

1. Find the difference between both y-coordinates. (6)

2. Find the difference between both x-coordinates. (3)

Divide the difference between y and x. y/x=2

The slope is 2.

Answer 2

The slope of line that passes through the points (2, -4) and (5, 2) is 2.

Step-by-step explanation:

Here's the required formula to find slope line :

`{\longrightarrow{\pmb{\sf{m = (y_2 - y_1)/(x_2 - x_1)}}}}`

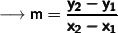
As per given question we have provided that :

`\begin{gathered}\footnotesize\rm {\underline{\underline{Where}}}\begin{cases}& \sf y_2 = 2\\& \sf y_1 = - 4\\ & \sf x_2 = 5\\ & \sf x_1 = 2\end{cases} \end{gathered}`

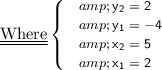
Substituting the values in the formula to find slope line that passes through the points :

`\begin{gathered}\qquad{\longrightarrow{\sf{m = (y_2 - y_1)/(x_2 - x_1)}}}\\\\\qquad{\longrightarrow{\sf{m = ((2) - ( - 4))/(5 - 2)}}}\\\\\qquad{\longrightarrow{\sf{m = (2 + 4)/(3)}}}\\\\\qquad{\longrightarrow{\sf{m = (6)/(3)}}}\\\\\qquad{\longrightarrow{\sf{m = 2}}}\\\\\qquad{\star{\underline{\boxed{\sf{\pink{m = 2}}}}}} \end{gathered}`

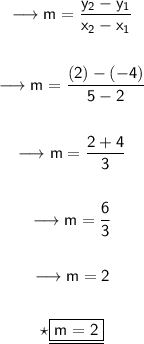
Hence, the slope of line that passes through the points (2, -4) and (5, 2) is 2.

`\rule{300}{2.5}`