Answer:
x = 6
Explanation:
Take the statement x varies directly as y and z
This means value of x is directly proportional to the value of y and z represented as x ∝ yz which can be represented as x = k.y.z where k is a constant known as the constant of proportionality
If x varies inversely as the square of r we represent this as x ∝ 1/r² or in equation form x = k/r²
Since the value of x is dependent on the values of y, z and jointly we have a single equation of proportionality:
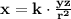
Given the values for x, y, z and r we can compute the proportionality constant and determine the value of x for any value of y, z or r
x = 16 when y = 3, z = 12 and r = 3
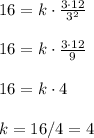
So the constant of proportionality is k = 4. Us this value in the proportionality equation along with y, z and r to get the value of x
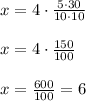
So x = 6 is the answer