Question

Factor completely

8x^2-6x-2x^3

Answer 1

2x(x-3)(-x+1)

Explanation:

Factor 2x from everything -> 2x(4x-3-x^2)

Reorder the terms -> 2x(-x^2+4x-3)

Write 4x as a sum -> 2x(-x^2+3x+x-3)

Factor out -x from -x^2+3x looks like -> 2x(-x(x-3)+x-3)

Factor out x-3 from the expression -> 2x(x-3)(-x+1)

Answer 2

`\displaystyle \large \boxed{ - 2x( x - 3)(x - 1)}`

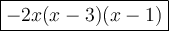
Explanation:

We are given the expression:

`\displaystyle \large{8 {x}^(2) - 6x - 2 {x}^(3)}`

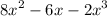
Notice how the expression has same x-term but not same degree, we can common factor out the x.

Factor using LCF (Least Common Factor which is 2x because 8 and 6 are multiples of 2.)

Therefore:-

`\displaystyle \large{2x(4x - 3 - {x}^(2)) }`

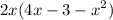
Inside the brackets, we can still factor. First, arrange the expression:-

`\displaystyle \large{2x( - {x}^(2) + 4x - 3) }`

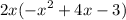
Factor -1 or negative sign out of the expression:

`\displaystyle \large{ - 2x( {x}^(2) - 4x + 3) }`

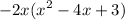
Factor x^2-4x+3 using two brackets.

What two numbers add/subtract each others and yield -4? The two numbers must multiply and yield 3 as well.

• -3 and -1 seem right value because -3-1 = -4 and -3(-1) is 3.

Thus:-

`\displaystyle \large{ - 2x( x - 3)(x - 1)}`

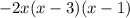
And we're done!