Answer:
:D
Explanation:
1.) One ticket out of eighty can be represented by a fractions, 1/80. To find the percentage, you can change 80 to 100 proportionally and then the difference (multiply/divide) to the 1 to find the percentage. You can also cross multiply to find the answer ("a")
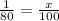
0.0125 is the chance of getting the ticket, and multiply by 100 to get percentage.
a = 1.25%
2.)
Same thing as #1, different equation :)
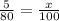
x = 6.25%
3.)
Same thing as #2, but now, on the bottom is not 80, but instead 70.

m = 7.14285714286%
m = 7.14%