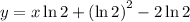Question

Find the equation of the line tangent to the graph of f(x) = (In x)² at x = 2.

Answer 1

`y = x \ln 2 +\left(\ln 2 \right)^2-2 \ln 2`

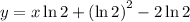
Explanation:

Differentiation is an algebraic process that finds the gradient of a curve.

At a point, the gradient of a curve is the same as the gradient of the tangent line to the curve at that point.

`\boxed{\begin{minipage}{5.4 cm}\underline{Chain Rule for Differentiation}\\\\If $y=f(u)$ and $u=g(x)$ then:\\\\$\frac{\text{d}y}{\text{d}x}=\frac{\text{d}y}{\text{d}u}*\frac{\text{d}u}{\text{d}x}$\\\end{minipage}}`

`\boxed{\begin{minipage}{4.5 cm}\underline{Differentiating $x^n$}\\\\If $y=x^n$, then $\frac{\text{d}y}{\text{d}x}=nx^(n-1)$\\\end{minipage}}`

`\boxed{\begin{minipage}{4.5 cm}\underline{Differentiating $\ln x$}\\\\If $y=\ln x$, then $\frac{\text{d}y}{\text{d}x}=(1)/(x)$\\\end{minipage}}`

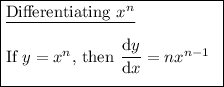
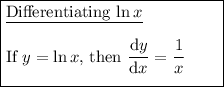
Differentiate the given function using the chain rule:

`\begin{aligned}f(x) & = \left(\ln x\right)^2\\\implies f'(x)& = 2\left(\ln x\right)^(2-1) \cdot \frac{\text{d}}{\text{d}x} \ln x\\& = 2\left(\ln x\right)^(1) \cdot (1)/(x)\\& = (2)/(x) \ln x \end{aligned}`

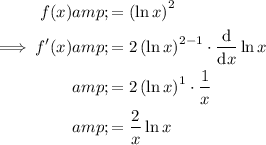
To find the gradient of the function at x = 2, substitute x = 2 into the differentiated function:

`\implies f'(2) = (2)/(2) \ln 2 = \ln 2`

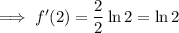
Therefore, the gradient of the function at x = 2 is ln(2).

Substitute x = 2 into the function to find the y-value of the point on the curve when x = 2:

`\implies f(2)= \left( \ln 2\right)^2`

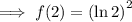
Slope-intercept form of a linear equation:

`y=mx+b`

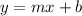
where:

• m is the slope.
• b is the y-intercept.

Substitute the point (2, (ln 2)²) and the found gradient into the slope-intercept formula and solve for b:

`\begin{aligned} y & = mx+b\\\implies \left(\ln 2 \right)^2 & = \ln 2 \cdot 2 + b\\\left(\ln 2 \right)^2 & =2\ln 2 +b\\b & = \left(\ln 2 \right)^2-2 \ln 2\end{aligned}`

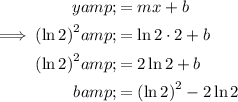
Therefore, the tangent has the equation:

`y = x \ln 2 +\left(\ln 2 \right)^2-2 \ln 2`