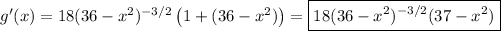Question

B) Let g(x) =x/2sqrt(36-x^2)+18sin^-1(x/6)

Find g'(x) =

Answer 1

I suppose you mean

`g(x) = \frac x{2√(36-x^2)} + 18\sin^(-1)\left(\frac x6\right)`

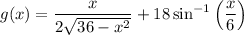
Differentiate one term at a time.

Rewrite the first term as

`\frac x{2√(36-x^2)} = \frac12 x(36-x^2)^(-1/2)`

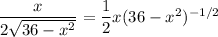
Then the product rule says

`\left(\frac12 x(36-x^2)^(-1/2)\right)' = \frac12 x' (36-x^2)^(-1/2) + \frac12 x \left((36-x^2)^(-1/2)\right)'`

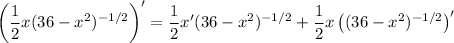
Then with the power and chain rules,

`\left(\frac12 x(36-x^2)^(-1/2)\right)' = \frac12 (36-x^2)^(-1/2) + \frac12\left(-\frac12\right) x (36-x^2)^(-3/2)(36-x^2)' \\\\ \left(\frac12 x(36-x^2)^(-1/2)\right)' = \frac12 (36-x^2)^(-1/2) - \frac14 x (36-x^2)^(-3/2) (-2x) \\\\ \left(\frac12 x(36-x^2)^(-1/2)\right)' = \frac12 (36-x^2)^(-1/2) + \frac12 x^2 (36-x^2)^(-3/2)`

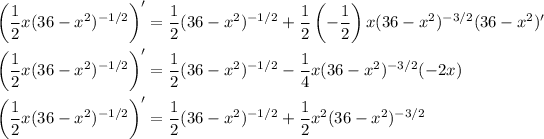
Simplify this a bit by factoring out
`\frac12 (36-x^2)^(-3/2)` :

`\left(\frac12 x(36-x^2)^(-1/2)\right)' = \frac12 (36-x^2)^(-3/2) \left((36-x^2) + x^2\right) = 18 (36-x^2)^(-3/2)`

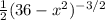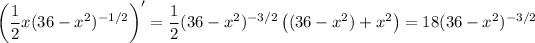
For the second term, recall that

`\left(\sin^(-1)(x)\right)' = \frac1{√(1-x^2)}`

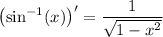
Then by the chain rule,

`\left(18\sin^(-1)\left(\frac x6\right)\right)' = 18 \left(\sin^(-1)\left(\frac x6\right)\right)' \\\\ \left(18\sin^(-1)\left(\frac x6\right)\right)' = (18\left(\frac x6\right)')/(√(1 - \left(\frac x6\right)^2)) \\\\ \left(18\sin^(-1)\left(\frac x6\right)\right)' = \frac{18\left(\frac16\right)}{\sqrt{1 - (x^2)/(36)}} \\\\ \left(18\sin^(-1)\left(\frac x6\right)\right)' = (3)/(\frac16√(36 - x^2)) \\\\ \left(18\sin^(-1)\left(\frac x6\right)\right)' = (18)/(√(36 - x^2)) = 18 (36-x^2)^(-1/2)`

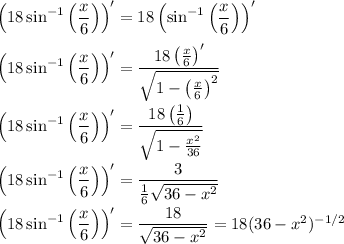
So we have

`g'(x) = 18 (36-x^2)^(-3/2) + 18 (36-x^2)^(-1/2)`

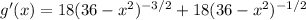
and we can simplify this by factoring out
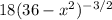`18(36-x^2)^(-3/2)` to end up with

`g'(x) = 18(36-x^2)^(-3/2) \left(1 + (36-x^2)\right) = \boxed{18 (36 - x^2)^(-3/2) (37-x^2)}`