Question

What is the index of refraction of a refractive medium if the angle of incidence in the air is 40 and the angle of refraction is 29?.

Answer 1

(1) sin 40° = n(sin 200⁰).

1. A ray of light traveling from air into crown glass strikes the surface at an angle of 30°.

Answer 2

We can often use Snell's Law to help us find the index of refraction of a refractive medium.

Snell's Law:
`(n_1)/(n_2)=(\sin(\theta_2))/(\sin(\theta_1))`

• 
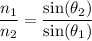
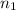  `n_1` = the refractive index of the first medium
• 
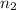  `n_2` = the refractive index of the second medium
• 
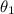  `\theta_1` = the angle of incidence
• 
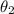  `\theta_2` = the angle of refraction

In this question, we're given the following:

• The angle of incidence is
  `40^\circ` ⇒
  `\theta_1=40^\circ`
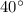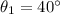
• The first medium is air, which has a refractive index of 1.0003 ⇒
  `n_1 = 1.0003`
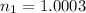
• The angle of refraction is
  `29^\circ` ⇒
  `\theta_2=29^\circ`
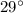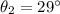
• Solve for
  `n_2`.

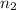Since we know we're solving for the index of refraction of the second medium, isolate
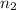`n_2` in Snell's Law:

`(n_1)/(n_2)=(\sin(\theta_2))/(\sin(\theta_1))\\\\\\(n_2)/(n_1)=(\sin(\theta_1))/(\sin(\theta_2))\\\\\\n_2=(\sin(\theta_1))/(\sin(\theta_2))*n_1`

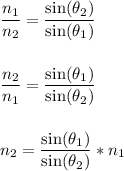
Plug in all the information we know and find
`n_2`:

`n_2=(\sin(40^\circ))/(\sin(29^\circ))*1.0003\\\\\\n_2\approx1.3263`

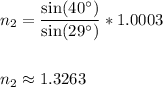
Answer

Therefore, the index of refraction of the refractive medium is approximately 1.3263.