Answer: Anything larger than the fraction 21/127
21/127 = 0.16535 approximately
=========================================================
Step-by-step explanation:
Let's solve each inequality for x
We'll start with the first inequality
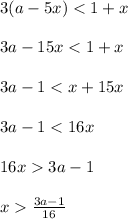
The variable x is larger than (3a-1)/16. If we knew what the value of 'a' was, then we could nail down the range of values for x more concretely.
Do the same for the second inequality
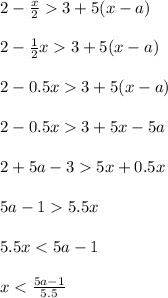
The variable x is also less than (5a-1)/(5.5)
--------------------------------------
At this point, we have found that
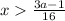 and
and
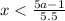
This means x is between those endpoints, excluding each endpoint
So we can form this compound inequality

This tells us the range of where x spans from.
---------------------------------------
If the endpoints are equal, aka the same value, then there's no way to have x have any solutions
So let's equate the endpoints and see what happens
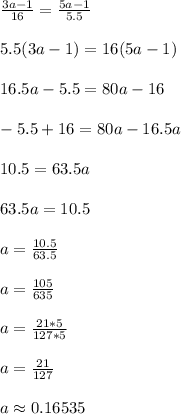
If 'a' is equal to that value, then the two endpoints of that compound inequality are completely identical; therefore, in that situation, we wouldn't have any solutions for x.
---------------------------------------
The question is: what happens if 'a' is some number smaller than 21/127?
Let's say a = 0
- The left endpoint would be (3a-1)/16 = (3*0-1)/16 = -0.0625
- The right endpoint would be (5a-1)/(5.5) = (5*0-1)/(5.5) = -0.1818 approximately
So we see that -0.0625 < x < -0.1818; however, upon closer inspection, you should find that such an interval makes no sense. Why not? Because -0.0625 is not smaller than -0.1818. It should be the other way around. No number exists that is between -0.0625 and -0.1818 (I recommend using a number line to help see why this is the case).
Therefore, anything smaller than a = 21/127 will result in having no solutions for x in the original system of inequalities.
--------------------------------------
Now let's try something larger than a = 21/127
Let's say we picked a = 1
- The left endpoint would be (3a-1)/16 = (3*1-1)/16 = 0.125
- The right endpoint would be (5a-1)/(5.5) = (5*1-1)/(5.5) = 0.7273 approximately
We end up with 0.125 < x < 0.7273 which is now valid because 0.125 is indeed smaller than 0.7273
Therefore, if a > 21/127, then we'll have those original system of inequalities lead to more than one solution for x.