Answer:
n = 18
Explanation:
The sides in a regular polygon are equal in length.
⇒ BC = CD
If BC = CD then ΔDCB is an isosceles triangle.
As the base angles of an isosceles triangles are equal:
⇒ ∠DBC = ∠BDC = 10°
Interior angles in a triangle sum to 180°.
⇒ ∠DBC +∠BDC + ∠DCB = 180°
⇒ 10° + 10° + ∠DCB = 180°
⇒ 20° + ∠DCB = 180°
⇒ ∠DCB = 180° - 20°
⇒ ∠DCB = 160°
Therefore, the interior angle of the regular polygon is 160°.
The interior angles of a regular polygon are equal in size.
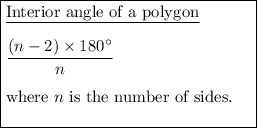
To find the number of sides, equate the formula to the found value of the interior angle and solve for n:
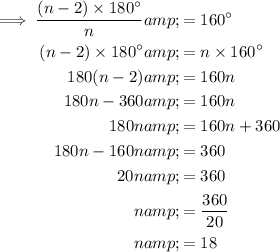
Therefore, the regular polygon has 18 sides.