Answer:
Approximately
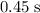 , assuming that air resistance is negligible and that
, assuming that air resistance is negligible and that
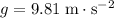 .
.
Step-by-step explanation:
The ball starts to fall the moment it rolls of the edge of the table.
- Let
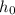 denote the initially height of this ball.
denote the initially height of this ball. - Let
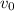 denote the initial vertical velocity of this ball.
denote the initial vertical velocity of this ball.
Assume that gravity is the only force acting on the ball during its fall (that is, there's no air resistance to slow the ball down.) The vertical acceleration of this ball during the fall would be constantly equal to
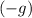 (negative because the ball is accelerating downwards.)
(negative because the ball is accelerating downwards.)
The following SUVAT equation would give the height
 of this ball at time
of this ball at time
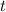 :
:
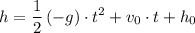 .
.
Since the table is horizontal, the vertical velocity of this ball would be
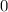 the moment it rolls of the edge. In other words:
the moment it rolls of the edge. In other words:
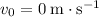 .
.
The initial height of this ball when it rolls of the table is
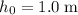 , same as the height of the table.
, same as the height of the table.
Hence, the height
 of this ball at time
of this ball at time
 would be:
would be:
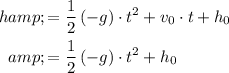 .
.
At
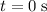 , the height of this ball would be
, the height of this ball would be
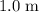 . The ball would be on the ground by the time
. The ball would be on the ground by the time
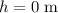 , Set the right-hand side of this equation to
, Set the right-hand side of this equation to
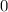 and solve for the time
and solve for the time
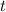 at which the ball is on the ground:
at which the ball is on the ground:
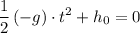 .
.
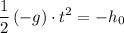 .
.
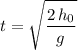 .
.
Substitute in the values
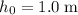 and
and
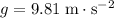 :
:
 .
.
In other words, the ball would be in the air for approximately
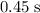 . (The initial horizontal velocity of this ball does not affect the duration of this fall.)
. (The initial horizontal velocity of this ball does not affect the duration of this fall.)