Explanation:
a negative exponent always means 1/...
so, e.g. 6^-2 means 1/(6²).
so,
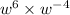
= w⁶/w⁴
that means that if w⁶w⁴ is already prefilled, we need to counteract the w⁴ in the numerator of the fraction.
it would have to be then w⁶w⁴/w⁸
because we need to end up with w⁴ in the denominator (bottom part). and the only way we can do that, if we need to keep w⁴ in the numerator (top) part, is to put these w⁴ multiplied by another w⁴ (4+4 = 8, as multiplied exponents are added).
that would give us the expanded form of
w×w×w×w×w×w×w×w×w×w
---------------------------------------
w×w×w×w×w×w×w×w
and the simplified form
w²/1
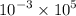
gives us the same problem.
it is actually 10⁵/10³
but if 10³10⁵ is already predefined, then we must use the same trick as before. we must end up with 10³ in the denominator, so to compensate for the 10³ in the numerator, we must extra multiply this into the denominator :
10³10⁵/(10³10³) = 10³10⁵/10⁶
the expanded form of this would be
10×10×10×10×10×10×10×10
------------------------------------
10×10×10×10×10×10
with the simplified form
10²/1
and again similar with
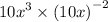
which is actually
10x³/(10x)² = 10x³/100x²
again, if 10x³×(10x)² is predefined in the numerator, we need to compensate in the denominator for these extra (10x)².
so, we need then to put
10x³(10x)²/((10x)²(10x)²) = 10x³(10x)²/(10x)⁴
the expanded form would then be
10×x×x×x×10×x×10×x
-----------------------------
10×x×10×x×10×x×10×x
and the simplified form would be
x/10
if these entries (as seen in the picture) in the "make exponent positive" column are from you and not predefined by your teacher, then we use the example of the first line.
and then we have as indicated
w⁶/w⁴
wwwwww / wwww
w²/1
10⁵/10³
10×10×10×10×10 / 10×10×10
10²/1
10x³/(10x)²
10×x×x×x / 10×x×10×x
x/10