Question

Subject: Mathematics

Concept: Algebra II · Solving Inequality
Question: Solve the x for following equation with two methods

`(1)/(x-1) \ \textgreater \ 4`

Answer 1

`\displaystyle (5)/(4) > x > 1`

`\displaystyle x \in \left(1, (5)/(4) \right)`

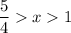
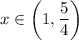
Explanation:

we would like to solve the following rational inequality

`\displaystyle (1)/(x - 1) > 4`

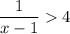
Note that we really CANNOT multiply both sides by x-1 as it can either be negative or positive however there're two methods of addressing this problem. Methods are as follows

Method-1:

In this method we would guess the answer by examining several values of x. Before we do so, we need to rearrange the inequality.

firstly, cancel 4 from both sides:

`\displaystyle (1)/(x - 1) - 4> 0`

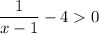
simplify:

`\displaystyle (1 - 4(x - 1))/(x - 1) > 0 \\ \\ (1 - 4x + 4)/(x - 1) > 0 \\ \\ ( - 4x + 5)/(x - 1) > 0`

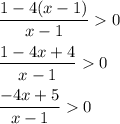
now we can examine different values of x to test where -4x+5/x-1 is greater than 0.

At x = -1, -4x+5/x-1 is less than 0

At x = 0, -4x+5/x-1 is less than 0

At x = 1 , -4x+5/x-1 is undefined

At x = 5/4 ,-4x+5/x-1 is equal to 0

At x = 2 , -4x+5/x-1 is less than 0

It tells us the image that

The inequality is true on the interval (1,5/4)

Method-2:

In this method, we would consider nothing but algebra to solve the inequality. Likewise method-1, we need to rearrange the inequality. As I've already shown how to rearrange the inequality, I am skipping the steps for now. so rearranging the inequality yields

`( - 4x + 5)/(x - 1) > 0`

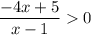
owing to algebra, we know that
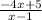`( - 4x + 5)/(x - 1)` would be greater than 0 in case

• Both the numerator and denominator is greater than 0
• Both the numerator and denominator is less than 0

thus it can be separated in two conditions

`\begin{cases} - 4x + 5 > 0\\\text{and} \\ x - 1 > 0\end{cases} \text{ \: \: \: or \: \: } \begin{cases} - 4x + 5 < 0\\\text{and} \\ \text{and}\\ x - 1 < 0\end{cases}`

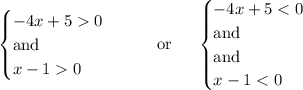
solve the inequalities:

`\begin{cases} x < (5)/(4) \\ \text{and} \\ x > 1\end{cases} \text{ \: \: \: or \: \: } \begin{cases} x > (5)/(4) \\ \text{and}\\ x < 1 \end{cases}`

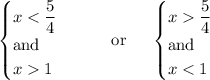
solve the "and" inequality or find the interception:

`x \in (1, (5)/(4) ) \text{ \: \: \: or \: \: }x \in \varnothing`

solve the "or" inequality or work out the union:

`x \in (1, (5)/(4) )`

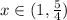
and we're done!