Question

Suppose the maximum power delivered by a car's engine results in a force of 16000 N on the car by the road. In the absence of any other forces, what is the maximum acceleration a this engine can produce in 1650-kg car?

Answer 1

Approximately
`9.7\; \rm m \cdot s^(-2)`.

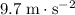Step-by-step explanation:

Assuming that there is no other force on this vehicle, the
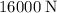`16000\; \rm N` force from the road would be the only force on this vehicle. The net force would then be equal to this
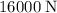`16000\; \rm N\!` force. The size of the net force would be
`16000\; \rm N\!\!`.

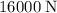Let
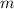`m` denote the mass of this vehicle and let
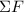`\Sigma F` denote the net force on this vehicle.

By Newton's Second Law of motion, the acceleration of this vehicle would be proportional to the net force on this vehicle. In other words, the acceleration of this vehicle,
`a`, would be:

`\begin{aligned}a &= (\Sigma F)/(m)\end{aligned}`.

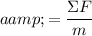For this vehicle,
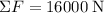`\Sigma F = 16000\; \rm N` whereas
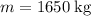`m = 1650\; \rm kg`. The acceleration of this vehicle would be:

`\begin{aligned}a &= (16000\; \rm N)/(1650\; \rm kg) \\ &= (16000\; \rm kg \cdot m\cdot s^(-2))/(1650\; \rm kg)\\ &\approx 9.7 \; \rm m \cdot s^(-2)\end{aligned}`.