Answer:
5. distance from B = 19.5 m, height of clock tower = 9.1 m
6.(i) 30.2 m
6.(ii) 71.1 m
Explanation:
Question 5
The given scenario can be modeled as two right triangles that have the same height (see attachment 1).
Define the variables
Let x = the distance between point B and the foot of the clock tower.
Let y = the height of the clock tower.
Use the given information and the tan trigonometric ratio to create equations for the height of the clock tower.
Tan trigonometric ratio
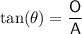
where:
 is the angle
is the angle- O is the side opposite the angle
- A is the side adjacent the angle
For triangle (point A):
Therefore:
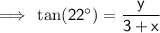
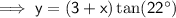
For triangle (point B):
Therefore:
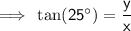
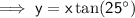
Substitute the equation for Triangle A into the equation for Triangle B and solve for x:
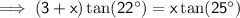
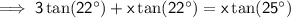

![\implies \sf 3\tan(22^(\circ))=x[\tan(25^(\circ))-\tan(22^(\circ))]](https://img.qammunity.org/2023/formulas/mathematics/high-school/x1ifh0qbrq0rx7gxe9zkgiaxnis43hjuko.png)


Therefore, the distance of B to the foot of the clock tower is 19.5 m (nearest tenth).
To find the height of the clock tower, substitute the found value of x into one of the found equations for y:
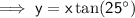
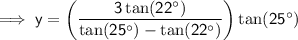
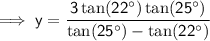

Therefore, the height of the clock tower is 9.1 m (nearest tenth).
-----------------------------------------------------------------------------------
Question 6
The given scenario can be modeled as two right triangles where the sum of their heights is 92 m (see attachment 2).
Define the variables
Let x = the distance between the foot of the building and the foot of the lamp post.
Let y = the height of the lamp post.
Use the given information and the tan trigonometric ratio to create equations for the height of the lamp post.
Tan trigonometric ratio
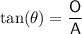
where:
 is the angle
is the angle- O is the side opposite the angle
- A is the side adjacent the angle
For the angle of elevation triangle:
Therefore:

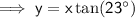
For the angle of depression triangle:
Therefore:
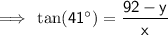
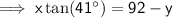
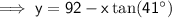
Substitute the equation for the angle of elevation triangle into the equation for depression triangle and solve for x:
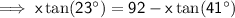
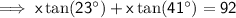
![\implies \sf x[\tan(23^(\circ))+\tan(41^(\circ))]=92](https://img.qammunity.org/2023/formulas/mathematics/high-school/46t0xzqc5223q6nd54z1ltgbo6ks587exa.png)
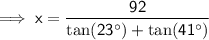
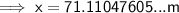
Therefore, the distance of the lamp post from the foot of the building is 71.1 m (nearest tenth).
To find the height of the lamp post, substitute the found value of x into one of the found equations for y:
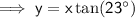


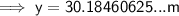
Therefore, the height of the lamp post is 30.2 m (nearest tenth).