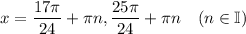Question

\cos ( 2x- \dfrac{ 3 \pi }{ 4 } ) = - \dfrac{ 1 }{ 2 }

Answer 1

`\displaystyle{x= (17\pi)/(24)+ \pi n, (25\pi)/(24)+\pi n \ \ \ (n \in \mathbb{I})}`

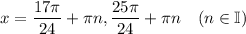
Explanation:

Given the cosine equation:

`\displaystyle{\cos \left(2x - (3\pi)/(4)\right) = -(1)/(2)}`

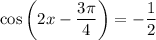
Let:

`\displaystyle{\theta = 2x - (3\pi)/(4)}`

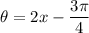
Then we will have:

`\displaystyle{\cos \theta = -(1)/(2)}`

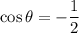
We know that cosθ is negative in second quadrant and third quadrant.

In second quadrant:

`\displaystyle{\pi - (\pi)/(3)}\\\\\displaystyle{=(3\pi)/(3) - (\pi)/(3)}\\\\\displaystyle{=(2\pi)/(3)}`

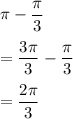
In third quadrant:

`\displaystyle{\pi + (\pi)/(3)}\\\\\displaystyle{=(3\pi)/(3) + (\pi)/(3)}\\\\\displaystyle{=(4\pi)/(3)}`

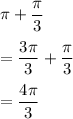
Therefore, we will have two solutions where:

`\displaystyle{\theta_1 = (2\pi)/(3)}\\\displaystyle{\theta_2 = (4\pi)/(3)}`

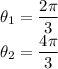
Convert from theta back to the original expression:

`\displaystyle{2x_1-(3\pi)/(4)= (2\pi)/(3)}\\\\\displaystyle{2x_2-(3\pi)/(4)= (4\pi)/(3)}`

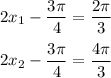
Convert two equations into one:

`\displaystyle{2x-(3\pi)/(4)= (2\pi)/(3), (4\pi)/(3)}`

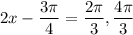
Since you do not specify the interval, add
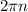`\displaystyle{2\pi n}` where
`\displaystyle{n \in \mathbb{I}}`.

`\displaystyle{2x-(3\pi)/(4)= (2\pi)/(3)+2\pi n, (4\pi)/(3)+2\pi n}`

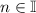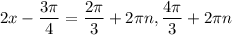
Solve the equation for x:

`\displaystyle{2x= (2\pi)/(3)+(3\pi)/(4)+2\pi n, (4\pi)/(3)+(3\pi)/(4)+2\pi n}\\\\\displaystyle{2x= (8\pi)/(12)+(9\pi)/(12)+2\pi n, (16\pi)/(12)+(9\pi)/(12)+2\pi n}\\\\\displaystyle{2x= (17\pi)/(12)+2\pi n, (25\pi)/(12)+2\pi n}\\\\\displaystyle{x= (17\pi)/(24)+ \pi n, (25\pi)/(24)+\pi n}`

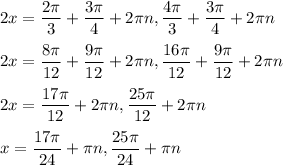
Therefore, the solution is:

`\displaystyle{x= (17\pi)/(24)+ \pi n, (25\pi)/(24)+\pi n \ \ \ (n \in \mathbb{I})}`