Question

Please help I Fr don’t understand

Answer 1

The given height function

`h(t) = -4.9t^2 + t + 148`

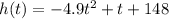
is the actor's height before opening the parachute. We have
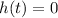`h(t)=0` for
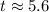`t\approx5.6` seconds after falling, so clearly the actor has pull the cord for some time
`t=t_0` with
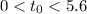`0<t_0<5.6` in order to safely land (as far as the film's audience is concerned, anyway).

At this time
`t=t_0`, the actor's height is

`h(t_0) = -4.9{t_0}^2 + t_0 + 148`

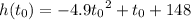
After opening the chute, his descent is slowed such that for any time
`t\ge t_0`, his height above the river is

`h(t) = a(t-t_0)^2 + b(t-t_0) + h(t_0)`

for some unknown coefficients
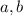`a,b`, which - not that it's important - represent the actor's acceleration and initial speed immediately after opening the chute.

Effectively, the actor's height
`h` at time
`t` is given by the function

`h(t) = \begin{cases} -4.9t^2 + t + 148 & \text{if } 0\le t<t_0 \\ a(t-t_0)^2 + b(t-t_0) + h(t_0) & \text{if } t\ge t_0 \end{cases}`

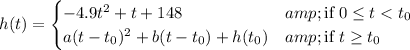
and we want to find the constants
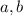`a,b` and the time
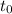`t_0` that satisfy the given conditions in the table.

We know the chute must be opened within the first 5.6 seconds, so the second cases applies for each given constraint.

`h(10) = a(10-t_0)^2 + b(10-t_0) - 4.9{t_0}^2 + t_0 + 148 = 38.8 \\\\ ~~~~ \implies 100a + 10b + (1-20a-b)t_0 + (a - 4.9) {t_0}^2 + 109.2 = 0 ~~~~~~~~ (1)`

`h(15) = a(15-t_0)^2 + b(15-t_0) - 4.9{t_0}^2 + t_0 + 148 = 25.8 \\\\ ~~~~ \implies 225a + 15b + (1-30a-b)t_0 + (a - 4.9){t_0}^2 + 122.2 = 0 ~~~~~~~~(2)`

`h(20) = a(20-t_0)^2 + b(20-t_0) - 4.9{t_0}^2 + t_0 + 148 = 8.8 \\\\ ~~~~ \implies 400a + 20b + (1-40a-b) t_0 + (a-4.9){t_0}^2 + 139.2 = 0 ~~~~~~~~ (3)`

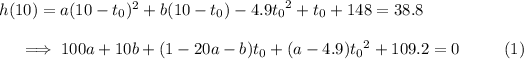
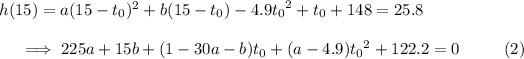
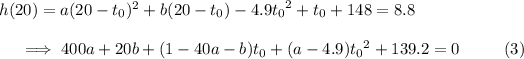
Solving these three equations for
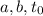`a,b,t_0`, you would find

`a = -0.08, b \approx -1.34, t_0\approx4.61`

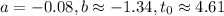
which tells us the actor opens the chute at a height of

`h(t_0) \approx -4.9(4.61)^2 +4.61  + 148 \approx \boxed{48.47}`

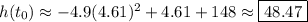
meters above the river.