Question

Consider the line y=7x-1. Find the equation of a line that is perpendicular and parallel to this line and passes through the point (2,-5)

Answer 1

Equation of perpendicular line:

`y = - (1)/(7) x - 4 (5)/(7)`

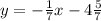
Equation of parallel line:

y= 7x -19

Explanation:

When an equation is written in the form of y= mx +c, we can easily identify its slope and y- intercept from its coefficient of x (value of m) and the value of c respectively.

y= 7x -1

Slope= 7

Y- intercept= -1

The product of the gradients of perpendicular lines is -1. Let the gradient of the perpendicular line be m.

m(7)= -1

`m = - (1)/(7)`

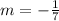
Substitute the value of m into the equation:

`y = - (1)/(7) x + c`

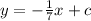
To find the value of c, substitute a pair of coordinates.

When x= 2, y= -5,

`- 5 = - (1)/(7) (2) + c`

`c = - 5 + (2)/(7)`

`c = - 4 (5)/(7)`

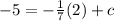
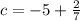
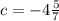
Thus the equation of the perpendicular line is
`y = - ( 1)/(7) x - 4 (5)/(7)`.

______

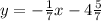Parallel lines have the same slope. Thus, m= 7.

y= 7x +c

To find the value of the y- intercept, substitute a pair of coordinates into the equation.

When x= 2, y= -5,

-5= 7(2) +c

-5= 14 +c

c= -5 -14

c= -19

Hence, the equation of the parallel line is y= 7x -19.