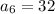Question

If f(1) =1 and f(n) = 2f (n-1) then find the value of f (6)

Answer 1

Answer: 32

==================================================

Step-by-step explanation:

Plug in n = 2

f(n) = 2*f(n-1)

f(2) = 2*f(2-1)

f(2) = 2*f(1)

f(2) = 2*1 ............. replace f(1) with 1, since f(1) = 1

f(2) = 2

Do so for n = 3

f(n) = 2*f(n-1)

f(3) = 2*f(3-1)

f(3) = 2*f(2)

f(3) = 2*2 ............. replace f(2) with 2, since f(2) = 2

f(3) = 4

Then replace every copy of n with 4.

f(n) = 2*f(n-1)

f(4) = 2*f(4-1)

f(4) = 2*f(3)

f(4) = 2*4 ............. replace f(3) with 4, since f(3) = 4

f(4) = 8

Repeat for n = 5

f(n) = 2*f(n-1)

f(5) = 2*f(5-1)

f(5) = 2*f(4)

f(5) = 2*8 ............. replace f(4) with 8, since f(4) = 8

f(5) = 16

Then finally n = 6

f(n) = 2*f(n-1)

f(6) = 2*f(6-1)

f(6) = 2*f(5)

f(6) = 2*16 ............. replace f(5) with 16, since f(5) = 16

f(6) = 32

The sequence is 1, 2, 4, 8, 16, 32, ...

This is the sequence of powers of 2. Each new term is found by doubling the previous term.

The closed form equation of this is
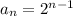`a_n = 2^(n-1)`. Plugging n = 6 into that will lead to
`a_6 = 32`