Question

A cylindrical can has a volume of 250 cm3 and is 10 cm tall. What is its diameter?

Answer 1

Approximately
`5.6\; {\rm cm}`.

Explanation:

The volume
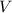`V` of a cylinder of height
`h` and radius
`r` is
`V = \pi\, r^(2)\, h`.

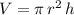Rearrange this equation to obtain an expression for the radius
`r` of this cylinder:

`\begin{aligned}r^(2) &= (V)/(\pi \, h)\end{aligned}`.

`\begin{aligned}r &= \sqrt{(V)/(\pi \, h)}\end{aligned}`.

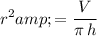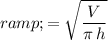For the cylinder in this question, it is given that
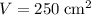`V = 250\; {\rm cm^(2)}` while
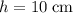`h = 10\; {\rm cm}`. The radius of this cylinder would be:

`\begin{aligned}r &= \sqrt{(V)/(\pi \, h)} \\ &= \sqrt{\frac{250\; {\rm cm^(3)}}{(\pi)\, (10\; {\rm cm})}} \\ &\approx 2.82\; {\rm cm} \end{aligned}`.

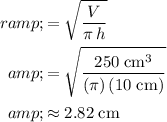The diameter
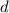`d` of a cylinder is twice the value of radius. Thus, the diameter of this cylinder would be:

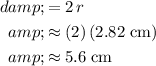`\begin{aligned} d &= 2\, r \\ &\approx (2)\, (2.82\; {\rm cm}) \\ &\approx 5.6\; {\rm cm}\end{aligned}`.