Question

HELP with Geometry PLEASES!! 100 points!!!

Answer 1

in order from images displayed, x = 20, x = 6, x = 5.5

Explanation:

4x - 8 + 6x - 12 = 180

10x -20 = 180

10x = 200

x = 20

5x - 1 = 29

5x = 30

x = 6

14x - 6 = 12x + 5

2x = 11

x = 5.5

Answer 2

Exercise 1: x is 20°.

Exercise 2: x= 6.

Exercise 3: x= 5.5.

Explanation:

Exercise 1.

1. Set up an equation.

If we where to addition both of the angles presented in the image, they have to sum up 180°, because is half a turn. Using this logic, we may add up both of the angles and equal them 180°:

`4x-8+6x-12=180`

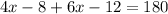
2. Solve the equation.

`4x-8+6x-12=180\\ \\4x+6x-8-12=180\\ \\10x=180+8+12\\ \\10x=200\\ \\(10x)/(10) =(200)/(10) \\ \\x=20`

3. Express the result.

Considering that the result of the equation was 20, there's enough evidence to sustain that the measure of angle x is 20°.

Exercise 2.

1. Create an equation.

If C is the midpoint of AQ, then AC must measure the same as CQ, hence, AC=CQ. In numerical terms:

`5x-1=29`

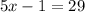
2. Solve the equation.

`5x-1=29\\ \\5x=29+1\\ \\5x=30\\ \\(5x)/(5) =(30)/(5) \\ \\x=6`

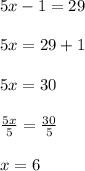
3. Express the result.

x= 6.

Exercise 3.

1. Create an equation.

It's basically the same as exercise 2, except that this time we are equating to an expression with a variable:

`14x-6=12x+5`

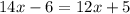
2. Solve the equation.

`14x-6=12x+5\\\\14x-12x=5+6\\ \\2x=11\\ \\(2x)/(2)=(11)/(2) \\ \\x=5.5`

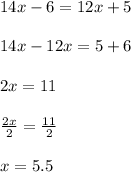
3. Express the result.

x= 5.5.