Answer:
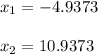
Explanation:
I'm assuming you need the solution of this equation, let's solve it!
1. Write the expression.
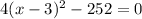
2. Solve the square parenthesis.
We are using the following property:
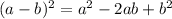
Let x be "a".
Let 3 be "b"
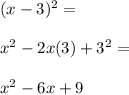
3. Take the result of the expansion and substitute it inside the parenthesis in the original expression.
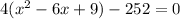
4. Make the associative multiplifation with 4.
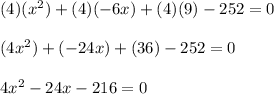
5.Simplify the expression.
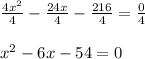
6. Find the roots.
Let's do it by applying the formula for solving quadratic equation. This is the formula:
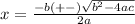
If you take a closer look, the equation has a ± symbol on the upper part to the right of -b, this means that either sum or substraction can be done to solve this equation. This means that we are going to get 2 solutions, always. Hence:
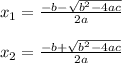
Tha values of a, b, and c are the following:
Since x² is being multiplied by 1, a= 1;
Since -6x is being multiplied by -6, b= -6;
Since -54 is a constant, c= .
Substitute in the 2 equations and find the roots (could be done with a calculator).
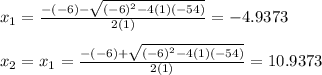
7. Express your results.
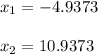 .
.