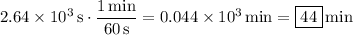Question

149,106 views

1 Answer

Lavrik · Answer 1 · 2023-11-02T02:59:16+0000

1. First, convert the model distance to base SI.

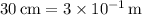
$30\,\mathrm{cm} = 3*10^(-1)\,\mathrm m$

Then the ratio of model distance to actual distance is

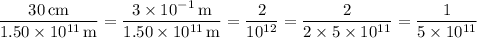
$(30\,\rm cm)/(1.50*10^(11)\,\rm m) = (3*10^(-1)\,\mathrm m)/(1.50*10^(11)\,\rm m) = (2)/(10^(12)) = (2)/(2*5*10^(11)) = (1)/(5*10^(11))$

or 1 : 5 × 10¹¹.

2. The model/actual distance ratio should be the same for each planet.

Mercury:

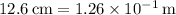
$12.6\,\mathrm{cm} = 1.26*10^(-1)\,\mathrm m$

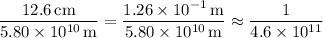
$(12.6\,\rm cm)/(5.80*10^(10)\,\rm m) = (1.26*10^(-1)\,\rm m)/(5.80*10^(10)\,\rm m) \approx (1)/(4.6*10^(11))$

or 1 : 4.6 × 10¹¹.

Venus:

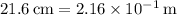
$21.6\,\mathrm{cm} = 2.16*10^(-1)\,\rm m$

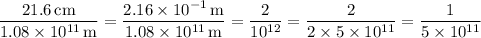
$(21.6\,\rm cm)/(1.08*10^(11)\,\rm m) = (2.16*10^(-1)\,\rm m)/(1.08*10^(11)\,\rm m) = (2)/(10^(12)) = (2)/(2*5*10^(11)) = \frac1{5*10^(11)}$

or 1 : 5 × 10¹¹.

Mercury's distance is the incorrect one. The correct model distance should be
such that

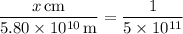
$(x\,\rm cm)/(5.80*10^(10)\,\rm m) = (1)/(5*10^(11))$

Solve for
.

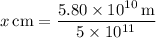
$x\,\mathrm{cm} = (5.80*10^(10)\,\rm m)/(5*10^(11))$

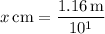
$x\,\mathrm{cm} = (1.16\,\rm m)/(10^1)$

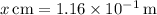
$x\,\mathrm{cm} = 1.16*10^(-1)\,\rm m$

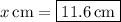
$x\,\mathrm{cm} = \boxed{11.6\,\rm cm}$

3.The actual distance for Mars is
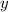such that

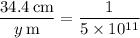
$(34.4\,\rm cm)/(y\,\rm m) = (1)/(5*10^(11))$

Solve for
.

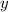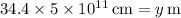
$34.4*5*10^(11) \,\mathrm{cm} = y\,\rm m$

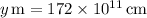
$y\,\mathrm m = 172 *10^(11)\,\rm cm$

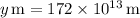
$y\,\mathrm m = 172 *10^(13)\,\rm m$

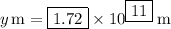
$y\,\mathrm m = \boxed{1.72} *10^{\boxed{11}}\,\rm m$

4. Divide the distance by the speed of light to recover the time.

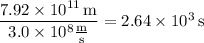
$(7.92*10^(11)\,\rm m)/(3.0*10^8(\rm m)/(\rm s)) = 2.64*10^3\,\mathrm s$

Convert to minutes.

$2.64*10^3\,\mathrm s \cdot (1\,\rm min)/(60\,\rm s) = 0.044*10^3\,\mathrm{min} = \boxed{44}\,\rm min$

Please log in or register to add a comment.