Answer:
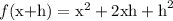
====================================================
Work Shown:

Step-by-step explanation:
I replaced each copy of x with x+h. Then I used the FOIL rule to expand things out and combine like terms. The distributive property or the box method are two other pathways you can take.