Answer:
1232 cm³
Explanation:
For a cone, the total surface area is
A = πrL + πr²
where L = slant height, r = radius
704 cm² = (25 cm)πr + πr²
πr² + 78.539816r - 704 = 0
Use the quadratic formula to solve for r.
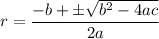
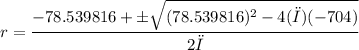
r = 7.00 or r = -32.00
We discard the negative value for the radius, and we keep r = 7.
Now we find the volume of a cone with r = 7 cm, L = 25
First, we find the height.
a² + b² = c²
(7)² + b² = (25)²
b = 24
height = 24 cm
V = (1/3)πr²h
V = (1/3)(π)(7 cm)²(24 cm)
V = 1232 cm³