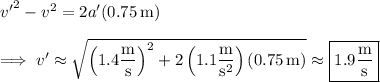Question

The frictionless system shown is released from rest. After the right-hand mass has risen 75 cm, the object of mass 0.50m falls loose from the system. What is the speed of the right-hand mass when it returns to its original position?​

Answer 1

Let
`a` be the acceleration of the masses. By Newton's second law, we have

• for the masses on the left,

`1.3mg - T = 1.3ma`

where
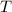`T` is the magnitude of tension in the pulley cord, and

• for the mass on the right,

`T - mg = ma`

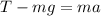
Eliminate
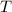`T` to get

`(1.3mg - T) + (T - mg) = 1.3ma + ma`

`0.3mg = 2.3ma`

`\implies a = (0.3)/(2.3)g \approx 0.13g \approx 1.3 (\rm m)/(\mathrm s^2)`

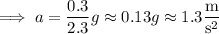
Starting from rest and accelerating uniformly, the right-hand mass moves up 75 cm = 0.75 m and attains an upward velocity
`v` such that

`v^2 = 2a(0.75\,\mathrm m) \\\\ \implies v \approx \sqrt{2\left(1.3(\rm m)/(\mathrm s^2)\right)(0.75\,\mathrm m)} \approx 1.4(\rm m)/(\rm s)`

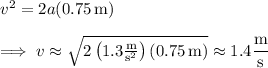
When the 0.5m mass is released, the new net force equations change to

• for the mass on the right,

`mg - T' = ma'`

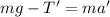
where
`T'` and
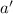`a'` are still tension and acceleration, but not having the same magnitude as before the mass was removed; and

• for the mass on the left,

`T' - 0.8mg = 0.8ma'`

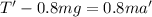
Eliminate
`T'`.

`(mg - T') + (T' - 0.8mg) = ma' + 0.8ma'`

`0.2mg = 1.8 ma'`

`\implies a' = (0.2)/(1.8)g = \frac19 g \approx 1.1(\rm m)/(\mathrm s^2)`

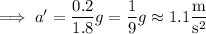
Now, the right-hand mass has an initial upward velocity of
`v`, but we're now treating down as the positive direction. As it returns to its starting position, its speed
`v'` at that point is such that

`{v'}^2 - v^2 = 2a'(0.75\,\mathrm m) \\\\ \implies v' \approx \sqrt{\left(1.4(\rm m)/(\rm s)\right)^2 + 2\left(1.1(\rm m)/(\mathrm s^2)\right)(0.75\,\mathrm m)} \approx \boxed{1.9(\rm m)/(\rm s)}`